No System

When we type some letters or words, the computer translates them in numbers as computers can understand only numbers. A computer can understand the positional number system where there are only a few symbols called digits and these symbols represent different values depending on the position they occupy in the number.

The value of each digit in a number can be determined using −

·        The digit

·        The position of the digit in the number

·        The base of the number system (where the base is defined as the total number of digits available in the number system)

Decimal Number System

The number system that we use in our day-to-day life is the decimal number system. Decimal number system has base 10 as it uses 10 digits from 0 to 9. In decimal number system, the successive positions to the left of the decimal point represent units, tens, hundreds, thousands, and so on.

Each position represents a specific power of the base (10). For example, the decimal number 1234 consists of the digit 4 in the units position, 3 in the tens position, 2 in the hundreds position, and 1 in the thousands position. Its value can be written as

(1 x 1000)+ (2 x 100)+ (3 x 10)+ (4 x l)

(1 x 10³)+ (2 x 10²)+ (3 x 10¹)+ (4 x l0⁰)

1000 + 200 + 30 + 4

1234

As a computer programmer or an IT professional, you should understand the following number systems which are frequently used in computers.

S.No.	Number System and Description
1	Binary Number System Base 2. Digits used : 0, 1
2	Octal Number System Base 8. Digits used : 0 to 7
3	Hexa Decimal Number System Base 16. Digits used: 0 to 9, Letters used : A- F

Binary Number System

Characteristics of the binary number system are as follows −

·        Uses two digits, 0 and 1

·        Also called as base 2 number system

·        Each position in a binary number represents a 0 power of the base (2). Example 2⁰

·        Last position in a binary number represents a x power of the base (2). Example 2^x where x represents the last position - 1.

Example

Binary Number: 10101₂

Calculating Decimal Equivalent −

Step	Binary Number	Decimal Number
Step 1	101012	((1 x 24) + (0 x 23) + (1 x 22) + (0 x 21) + (1 x 20))10
Step 2	101012	(16 + 0 + 4 + 0 + 1)10
Step 3	101012	2110

Note − 10101₂ is normally written as 10101.

Octal Number System

Characteristics of the octal number system are as follows −

·        Uses eight digits, 0,1,2,3,4,5,6,7

·        Also called as base 8 number system

·        Each position in an octal number represents a 0 power of the base (8). Example 8⁰

·        Last position in an octal number represents a x power of the base (8). Example 8^x where x represents the last position - 1

Example

Octal Number: 12570₈

Calculating Decimal Equivalent −

Step	Octal Number	Decimal Number
Step 1	125708	((1 x 84) + (2 x 83) + (5 x 82) + (7 x 81) + (0 x 80))10
Step 2	125708	(4096 + 1024 + 320 + 56 + 0)10
Step 3	125708	549610

Note − 12570₈ is normally written as 12570.

Hexadecimal Number System

Characteristics of hexadecimal number system are as follows −

·        Uses 10 digits and 6 letters, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

·        Letters represent the numbers starting from 10. A = 10. B = 11, C = 12, D = 13, E = 14, F = 15

·        Also called as base 16 number system

·        Each position in a hexadecimal number represents a 0 power of the base (16). Example, 16⁰

·        Last position in a hexadecimal number represents a x power of the base (16). Example 16^x where x represents the last position - 1

Example

Hexadecimal Number: 19FDE₁₆

Calculating Decimal Equivalent −

Step	Binary Number	Decimal Number
Step 1	19FDE16	((1 x 164) + (9 x 163) + (F x 162) + (D x 161) + (E x 160))10
Step 2	19FDE16	((1 x 164) + (9 x 163) + (15 x 162) + (13 x 161) + (14 x 160))10
Step 3	19FDE16	(65536+ 36864 + 3840 + 208 + 14)10
Step 4	19FDE16	10646210

Note − 19FDE₁₆ is normally written as 19FDE.

1.  Number Systems

Human beings use decimal (base 10) and duodecimal (base 12) number systems for counting and measurements (probably because we have 10 fingers and two big toes). Computers use binary (base 2) number system, as they are made from binary digital components (known as transistors) operating in two states - on and off. In computing, we also use hexadecimal (base 16) or octal (base 8) number systems, as a compact form for representing binary numbers.

1.1  Decimal (Base 10) Number System

Decimal number system has ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, called digits. It uses positional notation. That is, the least-significant digit (right-most digit) is of the order of 10^0 (units or ones), the second right-most digit is of the order of 10^1 (tens), the third right-most digit is of the order of 10^2 (hundreds), and so on, where ^ denotes exponent. For example,

735 = 700 + 30 + 5 = 7×10^2 + 3×10^1 + 5×10^0

We shall denote a decimal number with an optional suffix D if ambiguity arises.

1.2  Binary (Base 2) Number System

Binary number system has two symbols: 0 and 1, called bits. It is also a positional notation, for example,

10110B = 10000B + 0000B + 100B + 10B + 0B = 1×2^4 + 0×2^3 + 1×2^2 + 1×2^1 + 0×2^0

We shall denote a binary number with a suffix B. Some programming languages denote binary numbers with prefix 0b or 0B (e.g., 0b1001000), or prefix b with the bits quoted (e.g., b'10001111').

A binary digit is called a bit. Eight bits is called a byte (why 8-bit unit? Probably because 8=23).

1.3  Hexadecimal (Base 16) Number System

Hexadecimal number system uses 16 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F, called hex digits. It is a positional notation, for example,

A3EH = A00H + 30H + EH = 10×16^2 + 3×16^1 + 14×16^0

We shall denote a hexadecimal number (in short, hex) with a suffix H. Some programming languages denote hex numbers with prefix 0x or 0X (e.g., 0x1A3C5F), or prefix x with hex digits quoted (e.g., x'C3A4D98B').

Each hexadecimal digit is also called a hex digit. Most programming languages accept lowercase 'a' to 'f' as well as uppercase 'A' to 'F'.

Computers uses binary system in their internal operations, as they are built from binary digital electronic components with 2 states - on and off. However, writing or reading a long sequence of binary bits is cumbersome and error-prone (try to read this binary string: 1011 0011 0100 0011 0001 1101 0001 1000B, which is the same as hexadecimal B343 1D18H). Hexadecimal system is used as a compact form or shorthand for binary bits. Each hex digit is equivalent to 4 binary bits, i.e., shorthand for 4 bits, as follows:

Hexadecimal	Binary	Decimal
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
A	1010	10
B	1011	11
C	1100	12
D	1101	13
E	1110	14
F	1111	15

2.  Computer Memory & Data Representation

Computer uses a fixed number of bits to represent a piece of data, which could be a number, a character, or others. A n-bit storage location can represent up to 2^n distinct entities. For example, a 3-bit memory location can hold one of these eight binary patterns: 000, 001, 010, 011, 100, 101, 110, or 111. Hence, it can represent at most 8 distinct entities. You could use them to represent numbers 0 to 7, numbers 8881 to 8888, characters 'A' to 'H', or up to 8 kinds of fruits like apple, orange, banana; or up to 8 kinds of animals like lion, tiger, etc.

Integers, for example, can be represented in 8-bit, 16-bit, 32-bit or 64-bit. You, as the programmer, choose an appropriate bit-length for your integers. Your choice will impose constraint on the range of integers that can be represented. Besides the bit-length, an integer can be represented in various representation schemes, e.g., unsigned vs. signed integers. An 8-bit unsigned integer has a range of 0 to 255, while an 8-bit signed integer has a range of -128 to 127 - both representing 256 distinct numbers.

It is important to note that a computer memory location merely stores a binary pattern. It is entirely up to you, as the programmer, to decide on how these patterns are to be interpreted. For example, the 8-bit binary pattern "0100 0001B" can be interpreted as an unsigned integer 65, or an ASCII character 'A', or some secret information known only to you. In other words, you have to first decide how to represent a piece of data in a binary pattern before the binary patterns make sense. The interpretation of binary pattern is called data representation or encoding. Furthermore, it is important that the data representation schemes are agreed-upon by all the parties, i.e., industrial standards need to be formulated and straightly followed.

Once you decided on the data representation scheme, certain constraints, in particular, the precision and range will be imposed. Hence, it is important to understand data representation to write correctand high-performance programs.

Integer Representation

Ykfmab edfmktuba raprasamtdtkgmYkfmab 4&s igepjaeamt raprasamtdtkgmYkfmab >&s igepjaeamt raprasamtdtkgm

Integers are whole numbers or fixed-point numbers with the radix point fixed after the least-significant bit. They are contrast to real numbers or floating-point numbers, where the position of the radix point varies. It is important to take note that integers and floating-point numbers are treated differently in computers. They have different representation and are processed differently (e.g., floating-point numbers are processed in a so-called floating-point processor). Floating-point numbers will be discussed later.

Computers use a fixed number of bits to represent an integer. The commonly-used bit-lengths for integers are 8-bit, 16-bit, 32-bit or 64-bit. Besides bit-lengths, there are two representation schemes for integers:

1. Unsigned Integers: can represent zero and positive integers.
2. Signed Integers: can represent zero, positive and negative integers. Three representation schemes had been proposed for signed integers:
   1. Sign-Magnitude representation
   2. 1's Complement representation
   3. 2's Complement representation

You, as the programmer, need to decide on the bit-length and representation scheme for your integers, depending on your application's requirements. Suppose that you need a counter for counting a small quantity from 0 up to 200, you might choose the 8-bit unsigned integer scheme as there is no negative numbers involved.

Sign-Magnitude Representation

There are many schemes for representing negative integers with patterns of bits. One scheme is sign-magnitude. It uses one bit (usually the leftmost) to indicate the sign. "0" indicates a positive integer, and "1" indicates a negative integer. The rest of the bits are used for the magnitude of the number. So -24₁₀ is represented as:

1001 1000

The sign "1" means negative
The magnitude is 24 (in 7-bit binary)

Problems with Sign-Magnitude

There are problems with sign-magnitude representation of integers. Let us use 8-bit sign-magnitude for examples.

The leftmost bit is used for the sign, which leaves seven bits for the magnitude. The magnitude uses 7-bit unsigned binary, which can represent 0₁₀ (as 000 0000) up to 127₁₀(as 111 1111). The eighth bit makes these positive or negative, resulting in   -12710, ... -0, 0, ... 12710.

One pattern corresponds to "minus zero", 1000 0000. Another corresponds to "plus zero", 0000 0000.

There are several problems with sign-magnitude. It works well for representing positive and negative integers (although the two zeros are bothersome). But it does not work well in computation. A good representation method (for integers or for anything) must not only be able to represent the objects of interest, but must also support operations on those objects.

This is what is wrong with Roman Numerals: they can represent positive integers, but they are very poor when used in computation

What’s difference between 1’s Complement and 2’s Complement?

1’s complement of a binary number is another binary number obtained by toggling all bits in it, i.e., transforming the 0 bit to 1 and the 1 bit to 0.

Examples:

Let numbers be stored using 4 bits

1's complement of 7 (0111) is 8 (1000)
1's complement of 12 (1100) is 3 (0011)

2’s complement of a binary number is 1 added to the 1’s complement of the binary number.
Examples:

Let numbers be stored using 4 bits

2's complement of 7 (0111) is 9 (1001)
2's complement of 12 (1100) is 4 (0100)

These representations are used for signed numbers.

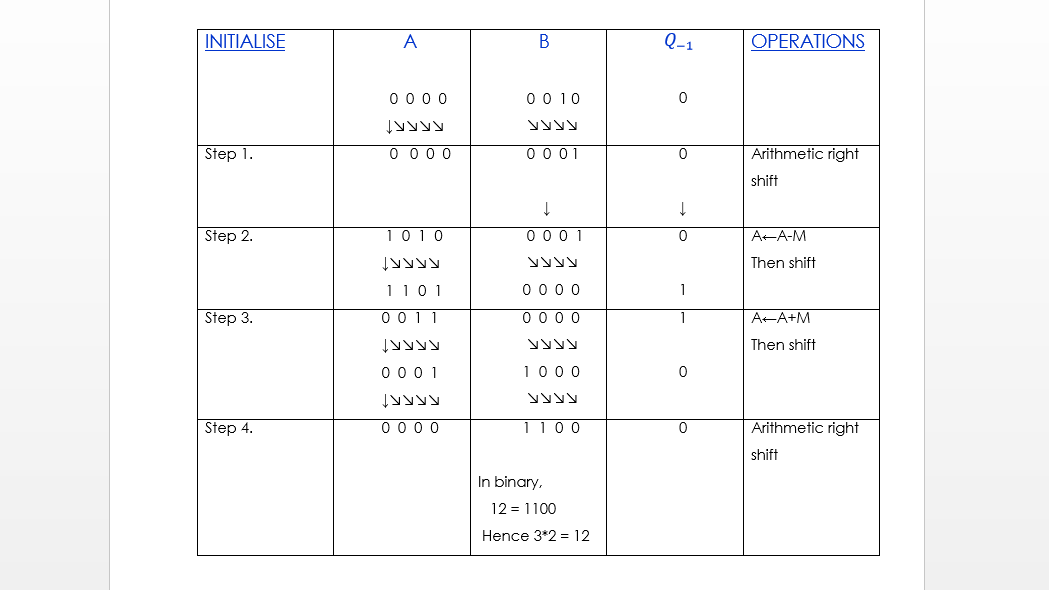
Booth's Multiplication Algorithm

Booth's algorithm is a multiplication algorithm that multiplies two signed binary numbers in 2's compliment notation.

---